等エントロピー過程

等エントロピー過程（isentropic process）とは、系のエントロピーが一定な熱力学過程。任意の可逆断熱過程は等エントロピー過程であることを証明できる。

背景

熱力学第二法則によれば次が成り立つ。

${\displaystyle \delta Q\leq TdS}$

ここで、${\displaystyle \delta Q}$は加熱によって系が獲得するエネルギー量、${\displaystyle T}$は系の温度、${\displaystyle dS}$はエントロピーの変化量である。等号があるのは、可逆過程の場合を意味している。可逆等エントロピー過程では、外部との熱エネルギーのやりとりがないので、断熱過程でもある。非可逆過程の場合、エントロピーは増大する。したがって系から熱を奪う（冷却する）ことで内部エントロピーを一定に保ち、等エントロピーな非可逆過程とする。したがって、非可逆等エントロピー過程は断熱過程ではない。

可逆過程の場合、等エントロピー変化は周囲の環境からその系を熱的に「絶縁」することでなされる。温度はエントロピーの熱力学的共役変数であり、したがって共役過程は等温過程である。等温過程では系は外界（恒温槽）と熱的に「接続」されている。

等エントロピー流

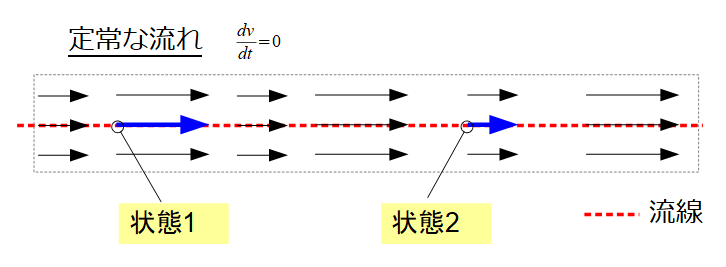
等エントロピー流 (isentropic flow) は、断熱的で可逆な流れである。すなわち、流れに対してエネルギーは加えられず、摩擦や散逸によるエネルギー損失も起きない。理想気体の等エントロピー流において、流線に沿った圧力、密度、温度の関係式が定義できる。

等エントロピー関係式の導出

閉鎖系において、系全体のエネルギー変化は、行った仕事と追加された熱の総和である。

${\displaystyle dU=dW dQ\,\!}$

体積の変化で系がなした仕事は次の式で表される。

${\displaystyle dW=-pdV\,\!}$

ここで${\displaystyle p}$は圧力、${\displaystyle V}$は体積である。エンタルピー (${\displaystyle H=U pV\,\!}$) の変化は次のようになる。

${\displaystyle dH=dU pdV Vdp=nC_{p}dT\,\!}$

可逆過程は断熱過程なので（すなわち、熱を外界とやり取りしない）、${\displaystyle dQ=0,dS=0\,\!}$ である。ここから次の重要な2つの式が導出される。

${\displaystyle dU=-pdV\,\!}$, および

${\displaystyle dH=Vdp\,\!}$ または ${\displaystyle dQ=dH-Vdp=0\,\!}$

${\displaystyle dQ=TdS\,\!}$ ⇒ ${\displaystyle dS=(1/T)dH-(V/T)dp\,\!}$

すると、比熱比は次のようになる。

${\displaystyle \gamma ={\frac {C_{p}}{C_{V}}}=-{\frac {dp/p}{dV/V}}\,\!}$

理想気体では${\displaystyle \gamma \,\!}$は定数なので、理想気体であることを前提として上の式を積分すると、次が得られる。

${\displaystyle pV^{\gamma }={\mbox{constant}}\,}$ であるから

${\displaystyle {\frac {p_{2}}{p_{1}}}=\left({\frac {V_{1}}{V_{2}}}\right)^{\gamma }}$

理想気体の状態方程式 ${\displaystyle pV=nRT\,\!}$ を使うと、次のようになる。

${\displaystyle TV^{\gamma -1}={\mbox{constant}}\,}$

${\displaystyle {\frac {p^{\gamma -1}}{T^{\gamma }}}={\mbox{constant}}}$

また、${\displaystyle C_{p}=C_{v} R}$（モル単位）が成り立つので、

${\displaystyle {\frac {V}{T}}={\frac {nR}{p}}}$ かつ ${\displaystyle p={\frac {nRT}{V}}}$

${\displaystyle S_{2}-S_{1}=nC_{p}\ln \left({\frac {T_{2}}{T_{1}}}\right)-nR\ln \left({\frac {p_{2}}{p_{1}}}\right)}$

${\displaystyle {\frac {S_{2}-S_{1}}{n}}=C_{p}\ln \left({\frac {T_{2}}{T_{1}}}\right)-R\ln \left({\frac {T_{2}V_{1}}{T_{1}V_{2}}}\right)=C_{v}\ln \left({\frac {T_{2}}{T_{1}}}\right) R\ln \left({\frac {V_{2}}{V_{1}}}\right)}$

以上から、理想気体の等エントロピー過程について、次が成り立つ。

${\displaystyle T_{2}=T_{1}\left({\frac {V_{1}}{V_{2}}}\right)^{(R/C_{v})}}$ または ${\displaystyle V_{2}=V_{1}\left({\frac {T_{1}}{T_{2}}}\right)^{(C_{v}/R)}}$

理想気体の等エントロピー関係式一覧

前提は次の通り。

${\displaystyle pV^{\gamma }={\text{constant}}\,\!}$

${\displaystyle pV=mR_{s}T\,\!}$

${\displaystyle p=\rho R_{s}T\,\!\,\!}$

ここで:

${\displaystyle p\,\!}$ = 圧力

${\displaystyle V\,\!}$ = 体積

${\displaystyle \gamma \,\!}$ = 比熱比 = ${\displaystyle C_{p}/C_{v}\,\!}$

${\displaystyle T\,\!}$ = 温度

${\displaystyle m\,\!}$ = 質量

${\displaystyle R_{s}\,\!}$ = 特定の気体の気体定数 = ${\displaystyle R/M\,\!}$

${\displaystyle R\,\!}$ = 標準気体定数

${\displaystyle M\,\!}$ = 特定の気体の分子量

${\displaystyle \rho \,\!}$ = 密度

${\displaystyle C_{p}\,\!}$ = 定圧比熱

${\displaystyle C_{v}\,\!}$ = 定積比熱

参考文献

• Van Wylen, G.J. and Sonntag, R.E. (1965), Fundamentals of Classical Thermodynamics, John Wiley & Sons, Inc., New York. Library of Congress Calatog Card Number: 65-19470

脚注・出典

関連項目

• 断熱過程